Find the shortest path in a graph
In the previous post, I have covered how to Find all paths in a graph adopting a breadth first search implementation. I had additionally added a method to filter out all the paths and return the shortest one from a starting to a destination node. That works but it’s not the most efficient way to calculate the shortest path in a graph. In this post I will use the same sample graph to implement the Dijkstra algorithm to more efficiently find the shortest path.
Here again is what the graph looks like:
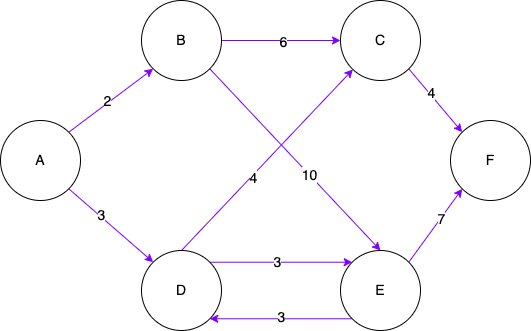
The idea is to store all nodes distances from the starting node as infinity into a distanceTable. I will then start exploring the graph edges from the starting node and for each edge, I will store its distance from the starting node into the distanceTable overwriting the distance anytime its distance cost is shorter than before. I will then repeat this action choosing to explore the unvisited node with the shortest distance from the starting node until all nodes have been visited.
At the end of the iteration I will have a table containing all the nodes from the graph with their relative shortest distance from the starting node.
In the previous implementation I used a queue to keep track of the probable paths. For this implementation I will use a Priority Queue. Here is my implementation of the priority queue in typescript. The first thing I need is to define the element that will be stored in the Priority Queue.
export default class Element<T> {
private element: T
private priority: number
constructor(element: T, priority: number) {
this.element = element;
this.priority = priority;
}
getElement(): T {
return this.element;
}
getPriority(): number {
return this.priority;
}
}The class above has a generic element T as element value and a priority number.
import Element from "./element";
export default class PriorityQueue<T> {
private elements: Array<Element<T>>
constructor() {
this.elements = [];
}
enqueue(element: T, priority: number): void {
const pe: Element<T> = new Element(element, priority);
for (let i = 0; i < this.elements.length; i++) {
if (this.elements[i].getPriority() > pe.getPriority()) {
this.elements.splice(i, 0, pe);
return;
}
}
this.elements.push(pe);
}
dequeue(): Element<T> {
const el: Element<T> | undefined = this.elements.shift();
if (el !== undefined) {
return el;
}
throw new Error("cannot dequeue empty queue");
}
isEmpty(): boolean {
return this.elements.length === 0;
}
getFirst(): Element<T> {
if (!this.isEmpty()) {
return this.elements[0];
}
throw new Error("cannot get first from empty queue");
}
getLast(): Element<T> {
if (!this.isEmpty()) {
return this.elements[this.elements.length - 1];
}
throw new Error("cannot get last from empty queue");
}
clear(): void {
this.elements = [];
}
}The methods to check out here are enqueue and dequeue. Enqueue adds a priority element to the queue making sure that the underlying elements array is ordered with the element with the highest priority (the lowest priority number) first. Dequeue will remove and return the first element in the array (which is the one with the highest priority). Now that I have sorted out my priority queue implementation I can focus on implementing the Dijkstra algorithm.
export default class Graph {
private adjacencyList: Map<string, List<Edge>>
constructor() {
this.adjacencyList = new Map();
}
//...
}The graph class has and adjacencyList map that is used to represents the nodes and their edges. Here is my implementation of Dijkstra:
dijkstra(start: string, end: string): Path {
// prepare the priority queue
const pq: PriorityQueue<string> = new PriorityQueue();
// prepare distanceTable to store shortest path
const distanceTable: Map<string, number> = new Map();
const unvisitedNodes: List<string> = new List();
// get all the nodes from the adjacency list
const entries: IterableIterator<string> = this.adjacencyList.keys();
let entry = entries.next();
while (entry.done === false) {
// set all the nodes as unvisited
unvisitedNodes.add(entry.value);
// set each node distance to infinity
distanceTable.set(entry.value, Infinity);
entry = entries.next();
}
// set the starting node distance to 0
distanceTable.set(start, 0);
let current: Element<string> = new Element(start, 0);
// keep looping until all the nodes have been visited
while(!unvisitedNodes.isEmpty()) {
// mark the current node as visited
unvisitedNodes.remove(current.getElement());
// visit all the edges
const edges: List<Edge> | undefined = this.adjacencyList.get(current.getElement());
edges?.values()
.forEach((edge) => {
// calculate the distance cost from the starting node
// by adding the current node cost with the edge distance
const cost: number = current.getPriority() + edge.getDistance();
// get the current cost for this node from the distanceTable
const currentConst: number = distanceTable.get(edge.getTo()) || Infinity;
if (cost < currentConst) {
// if the cost is less than the currentCost
// then replace it in the distanceTable
distanceTable.set(edge.getTo(), cost);
// enqueue the node to the priority list
pq.enqueue(edge.getTo(), cost);
}
});
if (pq.isEmpty()) {
if (!unvisitedNodes.isEmpty()) {
// since the priority queue is empty check whether there are still unvisited nodes
const unvisited = unvisitedNodes.get(unvisitedNodes.size() - 1);
// if so get the next unvisited node with its current distance or infinity
current = new Element(unvisited, distanceTable.get(unvisited) || Infinity);
continue;
} else {
// the priority queue is empty and there are no unvisited nodes
// return the path
return new Path(start, end, distanceTable.get(end))
}
} else {
// dequeue the priority queue when not empty to get the next current node to visit
current = pq.dequeue();
}
}
// done! return the path
return new Path(start, end, distanceTable.get(end))
}Here is a unit test I wrote before hand to verify the correctness of the implementation:
test('it should find the shortest path', () => {
const A: string = 'A';
const B: string = 'B';
const C: string = 'C';
const D: string = 'D';
const E: string = 'E';
const F: string = 'F';
graph.addNode('A')
.addNode('B')
.addNode('C')
.addNode('D')
.addNode('E')
.addNode('F')
.addEdge(A, B, 2)
.addEdge(A, D, 3)
.addEdge(B, C, 6)
.addEdge(B, E, 10)
.addEdge(C, F, 4)
.addEdge(D, C, 4)
.addEdge(D, E, 3)
.addEdge(E, F, 7)
.addEdge(E, D, 3);
const A_C: Path = graph.dijkstra(A, C);
expect(A_C.getDistance()).toBe(7);
const A_F: Path = graph.dijkstra(A, F);
expect(A_F.getDistance()).toBe(11);
const A_E: Path = graph.dijkstra(A, E);
expect(A_E.getDistance()).toBe(6);
});The complete codebase for this implementation can be found in the nodejs-series repository.