Find all paths in a graph
A few years back I was tasked with an interesting problem for a coding interview. Given a cyclic graph I had to find all possible paths from a starting node to a destination node. The graph was weighted and I also had to provide a method to find the shortest path. At first I thought to focus on finding all the available paths, then I could simply filter out all the results and return the shortest path. That’s what I am going to do in this implementation. I’ll cover the Dijkstra implementation in another post.
Here is what the graph looks like:
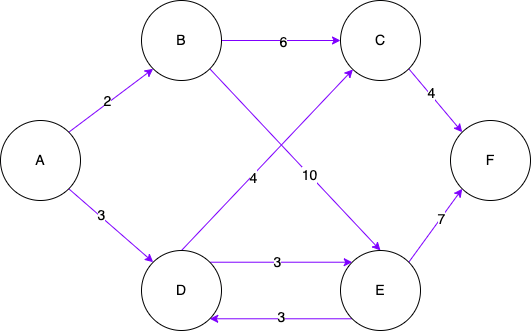
The circles represents the nodes, the arrows represents the direction of a connection and the number on the arrows represents the weight. Interesting to note, node D and node E are bi-directional. I am going to solve this problem with a BFS approach using a Queue. Breadth First Search is a recursion technique where neighbours nodes in a tree or a graph are explored before children nodes, I have briefly covered them in this article.
Let’s talk about the solution before we jump into the implementation. I am going to use a Queue data structure which follows FILO (first in last out). Say for instance we have a queue of integer with only a single entry with the value 1.

Now we want to add the value 2, the value will be added at the end of the collection.
If was to poll that queue now I would get 1 and the queue would be remaining with only the value 2.
What I want to do in this implementation is to poll the queue until it is not empty and if the last node in the path is not the destination, then I want to explore the neighbours and add to the queue a new list that includes previous nodes and the current neighbour node.
When I finally find a complete path, I will add that to a list and continue traversing until the graph has been completely explored. I am trying to find all paths from node A to node C. During the first iteration the queue will contain:

Polling the queue gives me back a list containing A since that’s not my destination node, I will start exploring A’s neighbours B and D adding two new lists including the previous node and the new neighbours [[A, B], [A, D]].

Polling the queue now gives me back a list containing A and B, since B is not the destination node, I will go through the same routine above and start exploring all of B’s neighbours. The queue will now contain: [[A, D], [A, B, C], [A, B, E]].
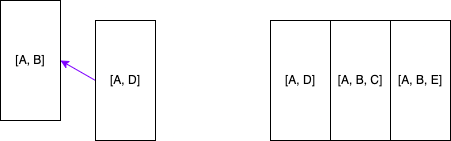
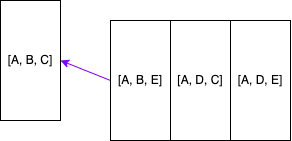
Polling the queue now gives me back a list containing A and D, since D is not the destination node, I will go through the same routine above and start exploring all of D’s neighbours. The queue will now contain: [[A, B, C], [A, B, E] [A, D, C], [A, D, E]].

Polling the queue now gives me back a list containing A, B and C, C is the destination node, therefore I save this path and keep polling the queue.
Hopefully this explanation was easy to follow. Here is how I have implemented my solution. I first created four different classes:
The Node represents a node in the graph.
public class Node {
/**
* Describes the way to identify a particular Node
*/
private final String name;
public Node(final String name) {
this.name = name;
}
public String getName() {
return name;
}
...
}The Edge represents the connection between two nodes in the graph with the weight.
public class Edge {
/**
* The distance value expressed as an Integer
*/
private final Integer distance;
/**
* The starting node
*/
private final Node from;
/**
* The destination node
*/
private final Node to;
public Edge(final Integer distance, final Node from, final Node to) {
this.distance = distance;
this.from = from;
this.to = to;
}
public Integer getDistance() {
return distance;
}
public Node getFrom() {
return from;
}
public Node getTo() {
return to;
}
...
}The Path represents a path as a list of edges.
public class Path {
/**
* represents the path from the starting edge to the final edge
*/
private final List<Edge> edges;
public Path() {
this.edges = new ArrayList<>();
}
public Path(List<Edge> edges) {
this.edges = edges;
}
/**
* Add the next Edge to the path
*
* @param edge the next edge to add to this path
* @return this
*/
public Path add(final Edge edge) {
this.edges.add(edge);
return this;
}
/**
* @return the sum of all the edges distance or null when there are no edges
*/
public Integer getLength() {
return this.edges.stream()
.map(Edge::getDistance)
.reduce(Integer::sum)
.orElse(null);
}
public List<Edge> getEdges() {
return edges;
}
...
}The Graph represents the graph as an adjacency list and implements methods to find all paths and the shortest path. The following is the logic for finding all the paths in the graph. In order to accomodate for easily query the lenght of a path, I wrote a little for loop that helps me with building the list of edges that is required for building the Path. Something worth noticing is that this solution works well with non cyclic graphs, to avoid incurring in an infinite recursion and a StackOverflowError I have added a check where if a path contains the same element more than once, it is discarded since nodes can only be visited one time.
private List<Path> findPaths(final Node from, final Node destination) {
// add the starting node to the probable path queue
probablePath.add(Lists.new(from));
// while there are probable paths to poll
while (!probablePath.isEmpty()) {
// poll the probable path
List<Node> path = probablePath.poll();
// get the last node in this path
Node lastNode = path.get(path.size() - 1);
// if the last node is equal to the destination we have a full path!
if (lastNode.equals(destination)) {
// start building the path by finding all the edges
List<Edge> edges = new ArrayList<>();
// loop the path
for (int i = 0; i < path.size() - 1; i++) {
// get the current node in the path
Node current = path.get(i);
// get the next node in the path
Node next = (i < path.size() - 2) ? path.get(i + 1) : destination;
// find the edge for this node in the adjacency list
Edge wanted = adjacencyList.get(current)
.stream()
// if the `to` node matches next then this is the edge we want
.filter(edge -> edge.getTo().equals(next))
// there will always be only one
.findFirst()
// zero is not possible, throw!
.orElseThrow();
// add the wanted edge to the list
edges.add(wanted);
}
// create a new path with the edges and add it to the paths list
paths.add(new Path(edges));
}
// since we are dealing with a cyclic graph, discard the path as soon as the
// lastNode appears more than once in the path (avoid a StackOverFlow)
else if (path.stream().filter(node -> node.equals(lastNode)).count() == 1) {
// find the neighbours for this node in the adjacency list
List<Edge> neighbours = adjacencyList.get(lastNode);
// for each neighbour node create a path from the previous path
for (Edge neighbour : neighbours) {
List<Node> nestedPath = new ArrayList<>(path);
nestedPath.add(neighbour.getTo());
// add the current path to the probablePath queue so it can be polled later
probablePath.add(nestedPath);
}
}
}
return paths;
}As I previously stated in this post, in order to find the shortest path, I have decided to simply reduce the list of paths to a single path with the shortest distance. The implementation looks like the following:
public Path shortestPath(final String fromName, final String toName) {
return allPaths(fromName, toName)
.stream()
.reduce((acc, com) -> (acc.getLength() < com.getLength() ? acc : com))
.orElse(null);
}Running the following test will help validating the solution.
class GraphTest {
private Graph graph;
@BeforeEach
void setUp() {
Node A = new Node("A");
Node B = new Node("B");
Node C = new Node("C");
Node D = new Node("D");
Node E = new Node("E");
Node F = new Node("F");
graph = new Graph();
graph.addNode(A)
.addNode(B)
.addNode(C)
.addNode(D)
.addNode(E)
.addNode(F)
.addEdge(A, new Edge(2, A, B))
.addEdge(A, new Edge(3, A, D))
.addEdge(B, new Edge(6, B, C))
.addEdge(B, new Edge(10, B, E))
.addEdge(C, new Edge(4, C, F))
.addEdge(D, new Edge(4, D, C))
.addEdge(D, new Edge(3, D, E))
.addEdge(E, new Edge(7, E, F))
.addEdge(E, new Edge(3, E, D));
}
@Test
void from_A_to_C() {
List<Path> paths = graph.allPaths("A", "C");
assertEquals(3, paths.size());
// sort by shortest first
List<Path> sorted = paths.stream()
.sorted(Comparator.comparing(Path::getLength))
.collect(Collectors.toList());
Path one = sorted.get(0);
assertNotNull(one);
assertEquals(7, one.getLength());
assertEquals("A -> D -> C", one.getReadableString());
Path two = sorted.get(1);
assertNotNull(two);
assertEquals(8, two.getLength());
assertEquals("A -> B -> C", two.getReadableString());
Path three = sorted.get(2);
assertNotNull(three);
assertEquals(19, three.getLength());
assertEquals("A -> B -> E -> D -> C", three.getReadableString());
Path shortestPath = graph.shortestPath("A", "C");
assertEquals(one, shortestPath);
assertEquals(paths, graph.getPaths());
graph.clearState();
assertTrue(graph.getPaths().isEmpty());
}
}The complete source code for the snippets illustrated in this post can be found in the java-series repo.




